TigerGraph Overview
A comprehensive overview of TigerGraph, highlighting its scalable system architecture and describing its unique data science capabilities.
Read it on meduim! : Link on meduim
In this article, we are going to present a general overview of TigerGraph. We will describe its architecture to showcase its capabilities and the problems it is designed to solve. We will also present its data model to understand better how the data is stored and organized within the system. Finally, we will present an example of using TigerGraph in the industry, highlighting its machine-learning support.
System Architecture
TigerGraph is a distributed, graph-oriented datastore with a massively parallel processing query engine. It differs from other similar datastores on the market due to its horizontally scalable architecture, which allows it to support the execution of workloads on big graphs of up to hundreds of billions of entities and 1 trillion relationships [1]. It supports native parallel query execution, enabling faster deep exploration of the data stored in TigerGraph. Its query language, GSQL, is a declarative, SQL-like query language with a lower learning curve for new developers in the field. It is also Turing complete, meaning that any query can be expressed using GSQL, unlike other similar query languages. In the following figure (figure 1), we present two types of GSQL queries.

The first query (Q1) is a simple filtering operation performed on all the graph vertices. The second query (Q2), however, lists some information about the edges of a set of paths filtered by a particular condition. The scanning of the paths in query Q2 is expressed using the graph pattern:
source-vertex-name-(edge-name)->target-vertex-name.
The figure below (Figure 2) represents the internal architecture of TigerGraph. The main building blocks of this architecture are (i) the graph storage engine (GSE), responsible for the physical storage and compression of graph data, and (ii) the graph processing engine (GPE), which offers parallel processing and graph partitioning capabilities, which are fundamental for the distribution and scalability of the system.
![Figure 2: TigerGraph internal architecture [2]](/assets/article_images/2023-05-23-tigergraph-overview/p2.png)
As shown in the same figure, Apache Zookeeper is used to coordinate the system’s different components and manage the distribution. It guarantees that the data is consistently replicated across the servers. TigerGraph also uses Apache Kafka for distributed message passing and queuing. Kafka communicates messages containing graph data, query results, and other information between the graph storage engine (GSE) and different instances of the graph processing engine (GPE). These two tools are fundamental in ensuring the reliability and scalability of the graph data store.
TigerGraph can be deployed on the cloud, on-premises, or on a hybrid infrastructure and can integrate different data sources, such as those from the Hadoop ecosystem or RDBMS solutions. It is also characterized by its high availability thanks to its replication and partitioning capabilities[3]. How will TigerGraph’s distribution features benefit the user in their graph-based data analytics? This point will be addressed in the last section (Applications).
TigerGraph Data Model
The data model in TigerGraph is graph-oriented. It is useful for representing connected data. It provides a data structure that helps to model complex relationships between different entities (real-world objects). In a graph, these entities are called vertices (or nodes) and are interconnected by edges. Edges are links that represent the relationship between these nodes. In TigerGraph, these data structures have attributes that can be atomic, structured (having a tuple type or container type [4]), or an accumulator. Accumulators are a type of attribute that stores the count or sum of a particular value. They are used to calculate metrics or statistics about the graph or to store intermediate results in a query. Examples of statistics that can be performed using accumulators include counting the occurrences of a value, comparing attributes with values, and calculating the average of an attribute. TigerGraph supports directed and undirected graphs, as well as weighted graphs.
Applications
Graph algorithms are often used in data analytics for tasks such as search, pathfinding, centrality or ranking, clustering, community detection, and similarity and classification. TigerGraph can support all these applications for large graphs thanks to its distributed nature and parallel processing query engine.
Search and pathfinding
These algorithms can help to search through large datasets quickly and efficiently in order to find specific information or patterns.
Graph search looks for vertices from a starting point by visiting its neighbours one hop at a time. Breadth-first search (BFS) and depth-first search (DFS) are examples of these search algorithms. The first searches the graph by visiting the neighbouring vertices first, and the second searches the path from a selected vertex until meeting the searched criteria and hops to another neighbour in case the search goal is not found. TigerGraph uses BFS in GSQL for graph-oriented queries thanks to its parallel processing capabilities.
Search algorithms allow the user to conduct deep link analysis in TigerGraph. Its query engine can search up to 10 hops away from the starting point, which is very efficient compared to earlier generation graph data stores that hardly achieve 3 or 2 hops search.
Another important search application specific to the graph data model is finding the “best” path between two vertices. A popular path-finding algorithm is the shortest path algorithm. Its goal is to minimize the distance between two vertices, and the distance can be measured as the number of hops or using weights assigned to the edges. Another popular path-finding algorithm is the A* algorithm, which is applicable to weighted graphs. Use cases for this type of algorithm include network traffic optimization and process optimization.
Graph centrality
Graph centrality (also known as influence, priority, or importance) techniques allow us to find the vertex that has the most connections in the graph: the closest vertex to the other neighbours or the most central vertex in the graph between other vertices (betweenness). It is a measure of how important a vertex is compared to its neighbours. The score used to calculate the centrality measure can also be used to rank the vertices of the graph, for example in the algorithm PageRank. Various scores are used to calculate centrality: (i) degree centrality, a measure of the number of neighbours for each vertex and the simplest centrality measure; (ii) betweenness centrality, the vertex with the number of paths between all the other vertices. These vertices are critical for connecting the different clusters in the graph and also belong to the shortest paths between the different vertices of the graph; (iii) closeness centrality, this score calculates all the shortest paths in the graph, then assigns the sum of the shortest path as a closeness degree for each vertex; (iv) eigen centrality, calculates the number of edges a vertex has as well as those of all of its neighbours one hop at a time and aggregates all of these measures; and finally, (v) PageRank, calculates the measure by counting the number of indegrees (incoming links from neighbours) beyond direct neighbours.
Community detection and clustering
In graph theory, communities or clusters are vertices that have common attributes or share a graph pattern. In the figure below (Figure 3), we have an example of two graph communities. The nodes in both communities share a common pattern of the following relationship: (person)-friends-(person).
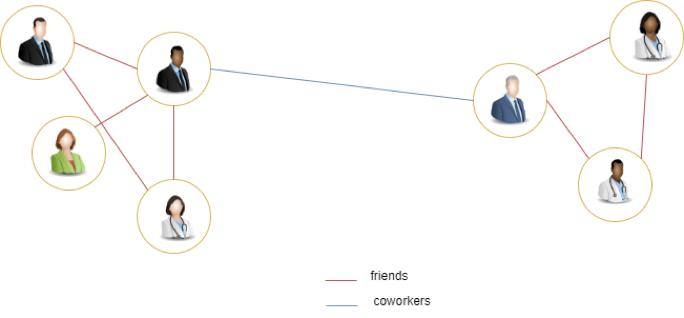
Community (cluster) detection uses similarity algorithms and graph patterns to group the vertices.
Recommendation
In TigerGraph, recommendation engines are built using clustering, similarity, and classification techniques. Similarity in graph algorithms applies to attributes as well as links and graph (/paths) patterns. In TigerGraph, similarity scores are defined as user-defined functions (UDFs). This allows the user to customize the algorithms and adapt them to his application-specific needs. There are various predefined similarity functions in the standard UDF library of TigerGraph, such as [5]: (i) the Euclidean similarity, which measures the distance between two points in n-dimensional space using the formula:
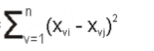
Where Xvi and Xvj are the attributes of two points Xi and Xj; (ii) the Pearson similarity, calculated using the Pearson correlation formula. The latter is calculated for two variables X and Y as the ratio between their covariance and the product of their standard deviation; and (iii) the cosine similarity, which is the measure of the cosine of the angle between two points represented in an n-dimensional space. It has the following formula:
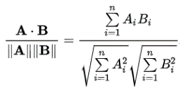
Where Ai and Bi are the attributes of two points A and B. In TigerGraph, it is possible to calculate three different variants of cosine similarity: single-sourced cosine similarity, calculated for two vertices using the attributes of their edges and those of the edges of their neighbours; batch cosine similarity, another variation of this algorithm that calculates the similarity between multiple pair of points in a single operation which optimizes the performance of the execution; and all pairs cosine similarity, which allows the user to calculate the cosine similarity for all the possible pairs in the graph. For most of these similarities, the attributes of the nodes/edges need to be transformed into numerical values and represented as a vector.
Conclusion
In this article, we presented a brief overview of TigerGraph and a summary of its graph algorithms for machine learning. For a deeper understanding of this tool, it is possible to explore multiple resources such as webinars and blogs about real-world use cases on their official website [6]. This blog post is the first of a two-blog series about Graph Analytics, and in the next one, we will showcase a practical example of using graph data science algorithms to solve problems.